[Up][Contents][Index]

Tutorial Examples

In order to help users learn how to use the system there are a number of example input files supplied with the program. They will have been installed on your computer if you followed the standard installation in the ./Manual/eg subdirectory. They can either be opened in the usual way for Windows programs (using [File|Open] or the button) or called directly from the manual by clicking on the relevant:
icon
You may need to configure your Browser to use OxCal to read view the model definition (.14i) files.

These examples are all taken to illustrate how the program can be used - they are not genuine archaeological examples. For real examples see Bronk Ramsey and Allen 1995, Bayliss et al 1997 and Needham et al 1998.

Plot Example 1

eg_plot1.14i

This example is simply a series of dates for calibration. Use is also made of the Line command to get a horizontal divide in the plot. Call the file up by clicking on the above icon. This should give you a window which looks something like this:

This window has four panes of which only the top two are visible. The right hand pane contains all of the items that you might wish to add to a plot and the left hand pane contains the plot as it has been constituted. To add extra items you would simply have to drag items from the right hand pane to the left. By dragging the frame up you should be able to see the bottom two panes too; in the left hand one of these is the text of the CQL command file which looks like this: 

Plot "Test Plot 1"
{
 R_Date "OxA-1000" 3860 60;
 R_Date "OxA-1001" 3956 60;
 R_Date "OxA-1002" 3890 50;
 Line;
 R_Date "OxA-1010" 3640 60;
 R_Date "OxA-1011" 3530 60;
 R_Date "OxA-1012" 3450 60;
 R_Date "OxA-1013" 3560 50;
};
To perform the calibration simply press the button (or use [File|Analyse...]). You should be able to see the plot organiser window which looks like this:

This window allows you to organise the plot as you wish (add labels, change orders ..etc). To actually generate the plot press the button or double click on the relevant icon within the plot organiser window.

To look at a single calibration plot simply double click on the relevant icon within the plot organiser window. To see all of the individual calibration plots press the button.

To get the results in text form press the button. This will open two text files: Log.14l contains a detailed description of the results, ranges etc; Tabbed.14l contains tabulated results which can be copied into spreadsheets, databases etc. Either of these can also be opened by double clicking on the or icon in the plot organiser window. The text results can be printed directly but there are no formatting options.

Any of the plots can be printed directly from the program or copied and pasted into word processor documents. Axes, labels and fonts can be changed at any stage through the [View] menu.

Plot Example 2

eg_plot2.14i

This example is also a plot but this time showing more types of chronological evidence including calendar dates, offset dates and an integrated probability distribution. The offsets will take some time to calculate. Also shown in this example are simulated radiocarbon dates which use the function R_Simulate. In these a calendar date is specified and the program generates the sort of radiocarbon date you might expect to get for a sample of this age with an error of the size specified. Much use has been made of these in the subsequent examples - they will give different values every time they are run. 

Plot "Example Plot 2"
{
 R_Date 1000 60;
 R_Date 900 60;
 R_Date 800 60;
 C_Date 1000 50;
 C_Date 1100 50;
 C_Date 1200 50;
 R_Simulate 1000 50;
 R_Simulate 1100 50;
 R_Simulate 1200 50;
 R_Date 1000 60; Offset 0 10;
 R_Date 1000 60; Offset 100 10;
 R_Date 1000 60; Offset 200 10;
 Before "before"
 {
  R_Date 1000 60;
 };
};
This example can be treated in the same way as the previous one. An additional operation you might try is to double click with the right mouse button on any of the individual icons. This will bring up the actual numerical data for the plots. This can be copied to a spreadsheet for further analysis or plotting should you wish.

Combine Example 1

eg_comb1.14i

This is a simple example of a combination of radiocarbon dates. 

Plot "Combine Example 1"
{
 R_Combine "Conquest"
 {
  R_Date 925 30;
  R_Date 875 30;
  R_Date 927 30;
  R_Date 924 30;
  R_Date 868 30;
  R_Date 936 30;
 };
 Axis 900 1200;
};
Once you have calculated this you might try recalculating it with some different values. To do this return to the input window and double click on the values you wish to alter - a dialog box will allow you to alter the values.

The Axis command has been used to define the limits of the x-axis in the final plot.

Combine Example 2

eg_comb2.14i

The example of a combination shows how gaps can be used to combine distributions with different relationships to the dated event. This is in effect a wiggle match. 

Combine "Combine Example 2"
{
 R_Date 1066 30;
 R_Date 1016 30; Gap 50;
 R_Date 966 30; Gap 100;
 R_Date 916 30; Gap 150;
 R_Date 866 30; Gap 200;
 R_Date 816 30; Gap 250;
};
When you have calculated the combination try viewing the results on the calibration curve using the button: the first page will probably have a large number of overlapping boxes but the second page should show how the combination has fitted the results to the calibration curve.

Sequence Example

eg_seq.14i

This example shows a typical application involving a sequence of items which contains a phase (ie. items with no known relative age differences). Analysing this will need MCMC sampling and will therefore take longer. The example is also set up to calculate the beginning, end and span of the phase as well as the span of the whole sequence: in the input file you should find folders () which contain these queries.

The enclosed sequence contains the obvious contstrain information. The outer sequence with the two boundaries is needed to ensure that the prior is for events Poisson distributed from a limited period of time.

Sequence "Sequence Example"
{
 Boundary;
 Sequence
 {
  R_Simulate 0 30;
  R_Simulate 50 30;
  R_Simulate 100 30;
  R_Simulate 150 30;
  R_Simulate 200 30;
  R_Simulate 250 30;
 };
 Boundary;
 Span "span seq";
};

Phase Example

eg_phase.14i

This example shows how Boundaries can be used to give estimates for the boundaries of phases. One of the dates generated here is fairly close to the modern end of the calibration curve and an information message may be displayed: use the [Retry] button to continue. Phases can be treated as sequential (with a possible gap) or abutting. In this case phases 1 and 2 are allowed to have a gap whereas phases 2 and 3 are assumed to be abutting. 

Sequence "Phase Example"
{
 Boundary "Start 1";
 Phase "1"
 {
  R_Simulate 950 50;
  R_Simulate 1000 50;
  R_Simulate 1050 50;
  Interval "Span 1";
  !calculates interval between
  !Start 1 and End 1
 };
 Boundary "End 1";
 Interval "Interval 1 to 2";
 Boundary "Start 2";
 Phase "2"
 {
  R_Simulate 1150 50;
  R_Simulate 1200 50;
  R_Simulate 1250 50;
  Interval "Span 2";
 };
 Boundary "2 to 3";
 !Phase 2 abuts phase 3
 Phase "3"
 {
  R_Simulate 1300 50;
  R_Simulate 1350 50;
  R_Simulate 1400 50;
  Interval "Span 3";
 };
 Boundary "End 3";
};
Note that, using this model, spans of phases should be calculated by using Boundary and Interval (or Difference) rather than Span which gives only the span of the dated events. For example Interval "Span 1" in this case gives the interval between Boundary "Start 1" and Boundary "End 1". The same distribution could have been obtained using the command: 
Difference "End 1" "Start 1"

Order Example

eg_order.14i

This shows a simple use of the facility for determining the order of events. It is also possible to put further constraints on these items to be ordered by using cross referencing or by placing the group as a whole within a sequence. 

Order "Order Example"
{
 R_Date "A" 1100 50;
 R_Date "B" 1000 50;
 R_Date "C" 900 50;
};
Note: As this is a fragment of code (which might form part of a larger model, no boundaries have been used; the program will warn you that there are no boundaries defined.

Terminus Ante Quem

eg_taq.14i

This example shows how a terminus ante quem can be used as a constraint. In this case the first event `OxA-1000' is known to be pre-conquest but we have no knowledge about the second event in the sequence. 

Sequence "Terminus Ante Quem Example"
{
 R_Date "OxA-1000" 970 40;
 TAQ
 {
  C_Date "Hastings" 1066;
 };
 R_Date "OxA-1001" 980 60;
 Correlation "correlation" "OxA-1000" "OxA-1001";
};
The example has also been set up to show how a correlation plot can be used. You can see from this plot the relationship between the two dated events and their relationship to the date of the conquest.

Note: As this is a fragment of code (which might form part of a larger model, no boundaries have been used; the program will warn you that there are no boundaries defined.

Difference and Interval Example

eg_diff.14i

This shows how the difference between two dates can be evaluated using Difference. In this case the same result has also been obtained by using the Interval command between the two dates in question to find the interval. 

Sequence "Difference Example"
{
 Boundary;
 R_Simulate 0 30;
 R_Simulate 50 30;
 R_Simulate "test1" 100 30;
 Interval "testi";
 R_Simulate "test2" 150 30;
 R_Simulate 200 30;
 R_Simulate 250 30;
 Boundary;
 Difference "testd" "test2" "test1";
};

Wiggle Matching Example 1

eg_dseq1.14i

The example of a piece of long lived wood from the iron age is taken here to show how such material could in principle be used to overcome the calibration problems in that period. 

D_Sequence "Wiggle Matching Example 1"
{
 First "first";
 R_Simulate -550 60; Gap 50;
 R_Simulate -500 60; Gap 50;
 R_Simulate -450 60; Gap 50;
 R_Simulate -400 60; Gap 50;
 R_Simulate -350 60; Gap 50;
 R_Simulate -300 60;
};
When you have performed the calibration try viewing the distributions on the calibration curve using the button. This will show how the data has been fitted to the calibration curve.

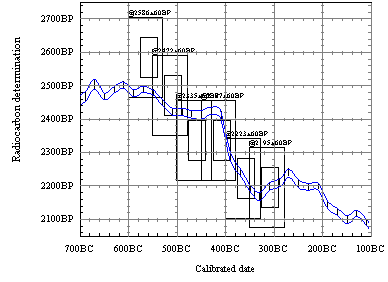
To get this to cover the range of the curve that you want double click on the plot (which will activate in-place editing) and then use either [View|Explore Curve] or [View|Adjust Axes].

Wiggle Matching Example 2

eg_dseq2.14i

This example is similar to the previous one except that it is set up to show that in principle other types of information can be included in such an analysis. 

D_Sequence "Wiggle Matching Example 2"
{
 First "first";
 R_Simulate 0 30; Gap 50;
 R_Simulate 50 30; Gap 50;
 C_Combine
 {
  C_Date 90 60;
  C_Date 100 60;
  C_Date 110 60;
 }; Gap 50;
 R_Simulate 150 30; Gap 50;
 R_Simulate 200 30; Gap 50;
 R_Simulate 250 30;
};

Wiggle Matching Example 3

eg_dseq3.14i

In this example the wiggle matching includes some unmeasured rings. The program then calculates ages for these rings using the defined gaps. 

D_Sequence "Wiggle Matching Example 3"
{
 First "first";
 Event "Zero"; Gap 50;
 R_Simulate -550 60; Gap 50;
 R_Simulate -500 60; Gap 50;
 Event "UnK"; Gap 50;
 R_Simulate -400 60; Gap 50;
 R_Simulate -350 60; Gap 50;
 R_Simulate -300 60; Gap 50;
 Event "Death";
};

Variable Sequence Example

eg_vseq.14i

This indicates the way in which approximately known age differences can be used for a sort of wiggle match. 

V_Sequence "Variable Sequence Example"
{
 R_Simulate 0 30; Gap 50 10;
 R_Simulate 50 30; Gap 50 10;
 R_Simulate 100 30; Gap 50 10;
 R_Simulate 150 30; Gap 50 10;
 R_Simulate 200 30; Gap 50 10;
 R_Simulate 250 30;
};
Note: This model does not contain any Boundaries; in this case they really are not necessary as long as the Gap constraints are fairly tight as this is more like a Wiggle Match; the program will warn that there are no boundaries.

Multiple Example

eg_mult.14i

This contains various examples which show how the program might be used for more complicated analysis. In particular, use is made of the fact that the main elements of a multi-plot are calculated one after another so that it is possible to use the results from the first main group in subsequent ones. 

Plot "Multiple Example"
{
 Phase
 {
  First "first";
  R_Simulate 140 30;
  R_Simulate 120 30;
  R_Simulate 130 30;
  R_Simulate 110 30;
  Last "last";
  Span "span phase";
 };
 After "after"
 {
  Prior "@first";
 };
 Before "before"
 {
  Prior "@last";
 };
 Combine
 {
  Prior "after";
  Prior "before";
 };
};