[Up][Contents][Index]
Performing the Analysis
Once the data has been entered the analysis can be performed simply
by pressing the 
button (or using the menu item
[File|Analyse...]). You might need to activate the top left hand
pane of the relevant input window before doing this. Recalculation
can be performed by the same
procedure but note that the data-files will be overwritten.
The first stage is the calibration of radiocarbon dates
(the methods used are similar to those used by
Stuiver and Reimer 1993 and
van der Plicht 1993, the error terms
in the calibration curve are taken into account;
also see
Dekling and van der Plicht 1993)
and calculation of other
distributions (these are
C_Date,
R_Date and
R_Simulate).
The distributions produced by this stage could be
referred to as 'prior' distributions (a term from Bayesian
statistics - see Bayes 1763 and
Doran and Hodgson 1975) because
the represent the state of our knowledge before any stratigraphic
information has been included.
Next all of the calculations which can be done analytically are
performed (these are
After,
Before,
C_Combine,
Combine,
Difference,
D_Sequence,
First,
Last,
Offset,
R_Combine,
Shift and
Sum).
See also [Mathematical Methods]
If it is required the second stage of analysis is automatically
started.
This stage uses a method called `MCMC Sampling' to incorporate the
stratigraphic evidence (see Buck et al 1992
and Gilks et at 1996}.
This method will be applied only if
Correlate,
Interval,
Order,
Span,
Sequence,
TAQ,
TPQ or
V_Sequence have been used.
This stage of the calculation can take quite a long time and a dialog
box is displayed showing progress.
It is quite normal for a few error messages to appear in this window
during the first few seconds of the analysis as the stratigraphic
order is resolved.
If the constraints you have entered are impossible to fulfill the
message `cannot resolve order' will persist and you should cancel
the analysis any try to sort out what is wrong (check first that
you have entered any sequences in chronological order -
oldest first).
During the sampling information is displayed indicating how it is
progressing.
A typical message would be something like:
Done: 43.2% Ok: 100.0% C>=98.6%
indicating that the sampling process is 43.2% complete,
all of the iterations fit the constraints and the worst convergence
value so far has been 98.6%.
Note that if the convergence is poor to begin with the program will continue
to lengthen the sampling time until it has risen above 95%.
See also [Mathematical Methods]
Obviously calculation times are very difficult to predict as they
depend both on the nature of the data and the computer being used.
With greater than 100MHz Pentium computers even quite complex models only take
a few minutes to run. Some models may require many more iterations
to converge properly than others. In general it is best to avoid
very deeply nested phases and boundaries.
If you are interested in the details of how the MCMC sample is being
performed it is possible to view the data file which defines the
relationships between the samples.
To do this you double click on the 
icon in the
plot organiser after the analysis has finished (see
example).
See also [File Formats]
Text versions of the results is always written out to two files
which can be viewed by pressing the
button
or double clicking on the relevant icons in the plot organiser
window. See the following examples:
The editor is only capable of dealing with log files up to 40kB long.
If the log file is longer than this the program will fail to open it and you
will have to use an alternative editor.
Some indication is clearly needed as to how well the data agree with
the stratigraphic constraints.
In the case of combinations of dates (prior to calibration) a
chi squared test is done (see Shennan 1988
p65).
An error message will be generated if the confidence limits drop
below 5%.
The results of the chi squared test are given on the plot at the head
of the group to be combined and will look something like:
R_Combine 913+-5 (df=3 T=1.9(5% 7.8))
The value given for T is the chi squared value calculated and the
value given in brackets is the level above which T it should
not rise (the degrees of freedom are given by df).
In the case of other types of analysis each posterior distribution is
given an agreement index which is displayed on the plot with the
sampled distribution name.
The mathematical definition for this is given in the appendix but
it indicates the extent to which the final (posterior) distribution
overlaps with the original distribution.
An unaltered distribution will have an index of 100% but it is
possible for the value to rise above this if the final distribution
only overlaps with the very highest part of the prior distribution.
If the value of this for any individual item is below 60% it may be
worth questioning its position in the stratigraphy and an error
message is generated (this level of disagreement is very similar
to that for the 5% level chi squared test).
See also [Mathematical Methods]
For a group of items (such as a sequence) it is possible to
define an overall agreement index which is a function of all of
the indices within the group (see the appendix on `Mathematical
Methods'). If this falls below 60% it may be worth
re-evaluating the assumptions made.
This overall agreement is shown on the plot at the top of the sampled
group and will be in a form like:
Sequence {A=100.9%(A'c=60.0%)}
where A is the calculated overall agreement index and
A'c is the level below which it is not expected to fall.
See also [Mathematical Methods]
In the case of combinations
(Combine and
D_Sequence) a
agreement index is calculated which is similar to the overall agreement
index.
Since all of these dates are correlated the criterion for agreement
is slightly different - again the program will indicate if the
agreement is poor (again this threshold is similar to the
5% chi squared test).
Such agreement indices will be shown in the plot in the form:
Combine test [n=4 A=124.4%(An=35.4%)]
where A is the calculated agreement index and
An is the value (dependent on n) below which it should
not fall.
Related to this agreement index is a value calculated if you
question a value for a combination
(Combine) or a wiggle
match (D_Sequence).
This value is again about 100% if the questioned item combines as
well as expected and decreases in proportion to the probability
if the combination is not very likely.
The value of this can also rise higher than 100% if the agreement
is unusually good.
See also [Mathematical Methods]
If you question the position of an item in a sequence a probability
is calculated instead of an agreement index. This will always be
less than or equal to 100% and gives the probability (given the prior)
distribution that the item comes from the particular place in the
stratigraphy selected. This value might be fairly low even if the
agreement would be fine when the constraints are very stringent and
the initial distribution wide.
See also [Mathematical Methods]
The convergence is a measure of how quickly the MCMC sampler is able to
give a representative and stable solution to the model. Details of the measure
used are given in the section on Mathematical Methods.
The number of iterations is automatically increased until the convergence is satifactory.
The convergence can also be studied in more detail by opting to store convergence data during
the sampling process (see Calculation options). If this is done
then after the calculation the convergence for individual distributions can be seen in square
brackets either in the plot organiser or on the plots themselves.
If convergence data has been included the actual sampling process can be observed by clicking on
the 
button or using [File|Individual plots]. The resultant plot will
look something like:
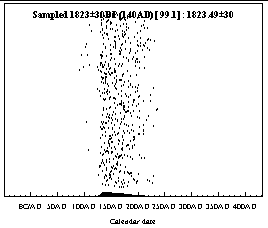
The dots each represent single samples. This is only a small section of the total sampling run
but it allows you to see if the model is getting 'stuck' in particular parts of the distribution.
There are several options relevant to the calculation methods and the
reporting format.
All relevant options can be accessed by using the
(or the [File|Analysis Options...] menu item). Options will be
automatically saved from session to session.
The most obvious option is the data file which is used for the
calibration curve.
To change this simply use the [Browse] button on the dialog box.Different calibration curves can be used for different samples using
Curve.
There is another option relating to the calibration curve: whether
or not a cubic function is used in interpolating the calibration
curve (see mathematical methods
for details) - this produces a smoother looking curve and
distributions but makes very little difference to any numerical values.
See also [Calibration Data] and
[Resolution]
The way in which calendar dates are reported and read in are affected
by the first two options. Calendar dates can be given as BP
(before 1950) instead of BC/AD; the strings `BP', `BC' and `AD' can
be omitted (using `-' for BC).
The third option relates to the way in which sequences are reported
and displayed: the normal order for sequences is oldest first
(chronological) but this can be reversed to correspond to
archaeological stratigraphy (youngest at the top); the data must
still be entered in chronological order; only
Sequence,
V_Sequence and
D_Sequence are affected by this option.
This defines the
resolution to which the calibration curve (and any calculated
distributions) are stored. Obviously calculations become slower
and the related files larger for a finer resolution. Assuming the
resolution is set at less than 20 years the results will still be
given to the nearest year above this they will be given to the
nearest 10 years.
______________________________________________
Storage Result
Resolution Resolution
_____________________
1 1
2 1
4 1
6 1
8 1
10 1
15 1
20 10
100 10
200 100
1000 100
_____________________
See also [Calibration Data]
Any combination of one two
and three sigma ranges can be selected. The ranges can be calculated
by the intercept method (only relevant to radiocarbon dates) or the
probability method. The ranges can be forced to be whole
(that is not divided up into segments); for the probability method
this produces `floruits' and in the case of the intercept method
the gaps in the ranges are simply removed giving one single range.
A option for rounding range values is provided. This will always round
ranges outwards and the resolution of the rounding is dependent on the
total range and the storage resolution.
______________________________________________
Total range Round to the nearest
______________________________________________
1 - 50 1 year
50 - 100 5 years
100 - 500 10 years
500 - 1000 50 years
1000 - 5000 100 years
... ...
______________________________________________
If the storage resolution is 4 years the ranges will be rounded to the
nearest 5 years regardless of how short the total range is, if rounding
is switched on.
If you prefer the resolution of rounding can be set by the user.
These are for advanced manipulation of the MCMC analysis.
The Uniform span
prior affects the way sequences of bounded events are treated (see
mathematical methods). This option
should normally be ON. It can be set to OFF for compatability with
previous (earlier than 3.2) versions of the program.
Inclusion of the convergence data is dealt with above.
The inverse square modelling option allows analysis on an inverse time scale
rather than a linear scale. This can be useful at the limit of radiocarbon
or when dealing with very long timescales (see
Bronk Ramsey 1998).
If the distributions after analysis are not sufficiently smooth, you may
wish to change the default number of iterations for the MCMC sampler.
This is normally set to 30k. Note that the program will automatically
increase the number of iterations if the convergence is poor.
The only option here is the default event type. This can be used for pasting in
events of different types from data on a spreadsheet. The command string for this
event will also not be shown on plots, log files etc.
These are the options set for the program as it is supplied and should
be set back to these values if you have problems.
________________________
Option Setting
____________________________
Calib curve intcal04.14c
Cubic interpolation on
Use BC/AD (not BP) on
Use -/+ for BC/AD off
Reverse plot order off
Resolution 5
1 Sigma ranges on
2 Sigma ranges on
3 Sigma ranges off
Probability method on
Round off ranges on
Round by auto
Whole ranges off
Uniform span prior on
Include conv data off
Inverse square modelling off
Default iterations 30k
Default event type R_Date
____________________________
The
resolution and (BP/AD/BC) options are also stored with each
CQL command file.
The form these options take is a string beginning with a `-'.
The forms of this string are shown below and can be
entered in this form in the command line version of the program.
-afilename append log to a file*
-b1 BP -b0 BC/AD
-cfilename use calibration data file
-d1 plot distributions -d0 no plot
-fn default iterations for sampling in thousands
-g1 +/- -g0 BC/AD/BP
-h1 whole ranges -h0 split ranges
-in resolution of n
-ln limit on number of data points in calibration curve (see Resolution)
-m1 macro language -m0 simplified entry
-n1 round ranges -n0 no rounding
-o1 include converg info -o0 do not include
-p1 probability method -p0 intercept method
-q1 cubic interpolation -q0 linear interpolation
-rfilename read input from a file+
-s11 1 sigma ranges -s10 range not found
-s21 2 sigma ranges -s20 range not found
-s31 3 sigma ranges -s30 range not found
-t1 terse mode -t0 full prompts
-u1 uniform span prior -u0 as in OxCal v2.18 and previous
-v1 reverse sequence order -v0 chronological order
-wfilename write log to a file*
-yn round by n years -y0 automatic rounding
* Note that with either of these options the tabbed results will then be sent
to the console output and can therefore be redirected to a file or a pipe;
the standard DOS redirection > or >> can be used instead if only the log file
needs redirecting.
+ Note that the standard DOS redirection < can also be used.
Full log file
Tabulated results (single ranges)